最短路径钉绳法模拟
本文最后更新于 2024-07-28,文章内容可能已经过时。
寻找最佳路径
你发现没有,最近一段时间以来的很多期内容,都涉及用物理方法与数学的联系,机械装置与数学的关系,等等。比如:
《培根说过:数学让人精细》——物理模型摸拟数学中正三角形与正方形转化拼接问题。
《我画圆,却也画出了直线》——用到机械连杆装置演示数学中的反演概念。
《费马点与学校选址问题》——用到力学中的势能最小原理进行学校选址。
本期介绍一种物理方法或叫实物方法,用它来寻找最短路径。这种方法在比较简单的情况下可以尝试一下,很有新意,但有些费时。如果有那么多时间,最长路径也走完了。这个方法在现代社会已不实用了,我们有导航系统了。但什么叫最短,本题是一个很好的实物模拟,仍然是很有创意的。也说不好什么地方会用到这个思路解决其他什么问题呢。我们暂且用一首日本民歌《拉网小调》形容我们的这种方法。(我对比听了不同的演唱版本,比较喜欢胡松华演唱的。)
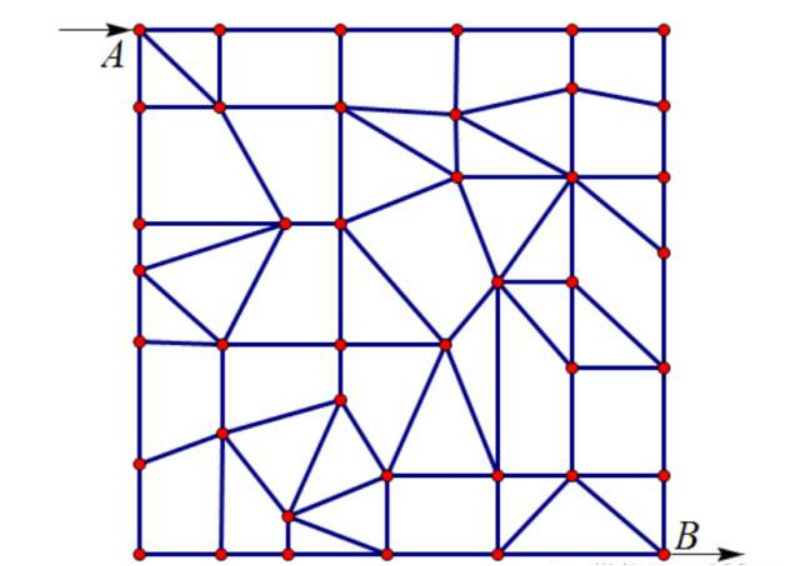
从地图左上角的A地要去地图右下角的B地。这之间要穿过很多的道路,若用计数原理计算的话,可能会有很多种走法。如何选择一条最短路径,看来不是很容易。
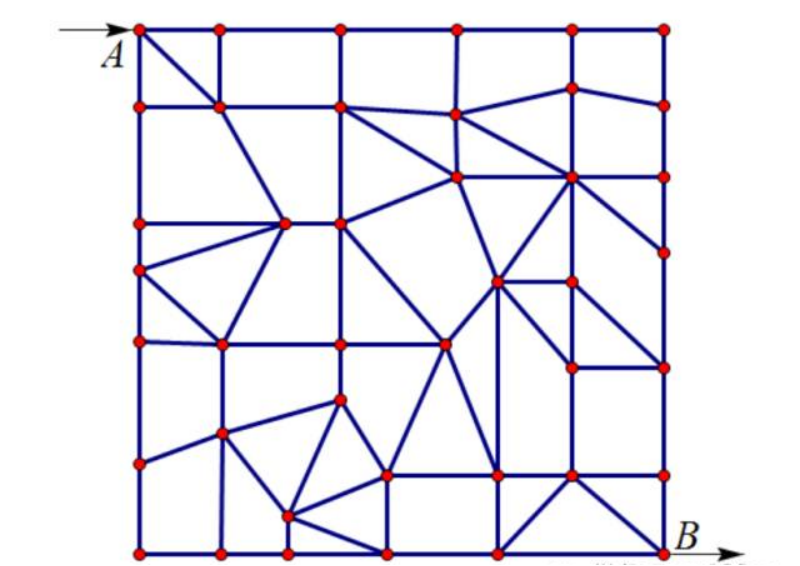
我把地图平铺在一块木板上,固定住不让它移动。在A地和B地钉上钉子,然后在可能经过的交叉路口也钉上钉子。钉子与钉子之间有路相连时,就用绳子相连。注意一定要绷紧。只要有路相连就要用绳子连接。把每一段绳子都染以不同的颜色,用手机拍照下来。每个钉子处都可能会连接有几根绳子。最终我们是要把钉子取走的,但每个钉子取走时,需要把这个钉子处连接的几条绳子的端点连接在一起成为固定的结点(死结)。最后,就相当于“织”成了一张网。
然后,我们一手抓住A端,另一手抓住B端,把网拉紧(可以边拉边唱“拉网小调”,嘿嘿),那么,一定会有几段绳子是绷紧的。用手机拍照下来,主要是把绷紧的几段绳子的颜色拍照下来。那么, 我们说,绷紧的那几段绳子原来对应的线路就是最短路径。
我们熟知的最短路径算法有五种 :
1:Dijkstra 2:Floyd 3:Bellman-Ford 4:SPFA 5:A*
此方法的难点在于如何模拟钉绳法这个过程(模拟后的优秀程度也许不如上面五种),如果写出来还像上面五种一样,那就失去了模拟的意义。
- 感谢你赐予我前进的力量


